Drucker-Prager (DP)
Le modèle de matériau de Drucker-Prager est le modèle de matériau le plus simple, qui peut être adopté pour la modélisation d'une réponse non linéaire des sols. Contrairement au modèle de Mohr-Coulomb, la surface de charge de Drucker-Prager est lisse et, dans l'espace des contraintes principales, elle se présente sous la forme d'un cône cylindrique. Comme le montre la figure ci-dessous, la surface de charge, tout comme dans le modèle de Mohr-Coulomb, dépend de la contrainte effective moyenne σmeff. La version actuelle du modèle mis en œuvre dans GEO5 MEF repose sur l'hypothèse d'une extension triaxiale. En d'autres termes, la projection de la surface de charge fDP dans un plan déviatorique passe par les sommets internes de l'hexagone de Mohr-Coulomb, θ = - 30°, où θ est l'angle de Lode.
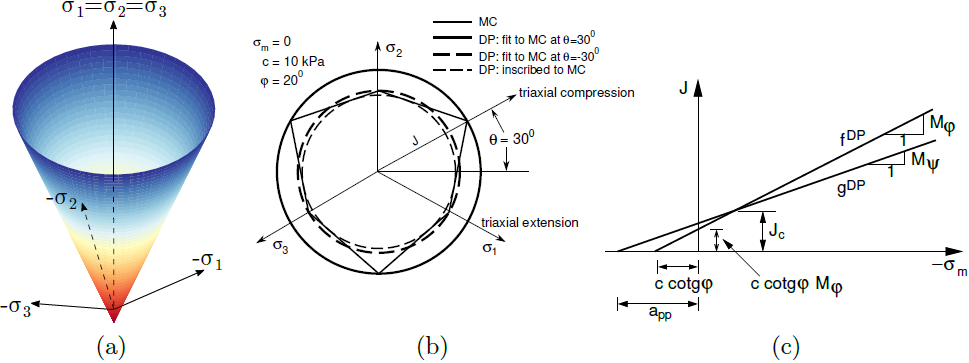 a) surface de charge dans l'espace des contraintes principales, b) projection dans le plan déviatorique c) dans le plan mériden
a) surface de charge dans l'espace des contraintes principales, b) projection dans le plan déviatorique c) dans le plan mériden
Le modèle de Drucker-Prager permet de prendre en compte la dilatance du matériau (évolution des déformations plastiques volumétriques positives pendant le cisaillement plastique) en introduisant l'angle de dilatance ψ. L'évolution des déformations plastiques est en général contrôlée par le potentiel plastique gDP. Alors que la pente de la surface de charge dans le plan méridien est donnée par l'angle de frottement interne Mφ = Mφ(φ), la pente de la surface de potentiel plastique dépend de l'angle de dilatance Mψ = Mψ(ψ). La condition ψ = φ correspond à la règle d'écoulement associé, sinon la règle d'écoulement non associé est considérée. De plus amples détails peuvent être trouvés dans le manuel théorique. Comme le sol finit par atteindre ce que l'on appelle l'état critique (augmentation nulle de la déformation plastique volumétrique pendant le cisaillement plastique), il est souhaitable de limiter l'étendue de la dilatance. Cela nécessite l'introduction de l'indice des vides maximal emax, pour lequel l'atteinte de l'état critique ψ = 0 est attendue. Un exemple illustratif est présenté ici. La façon dont le choix de la valeur de l'angle de dilatance influence la prévision de la réponse du sol par rapport à son comportement réel est présentée ici. Par souci de clarté, nous présentons, sur la figure suivante, une représentation graphique de l'évolution de la déformation volumétrique en fonction de l'angle de dilatance.
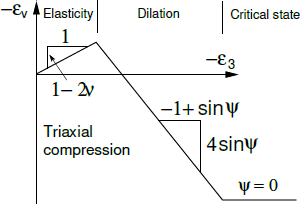 Évolution de la déformation plastique volumétrique avec coupure de la dilation
Évolution de la déformation plastique volumétrique avec coupure de la dilation
Les paramètres matériels de base définissant le modèle de Drucker-Prager sont énumérés dans le tableau suivant. Ces paramètres peuvent être adoptés lors de l'analyse en conditions drainées ou en cas de conditions non drainées, Type (1) : analyse en contraintes effectives (cef, φef). En choisissant le Type (2) : analyse en contraintes effectives (Su), la valeur de la cohésion effective c est remplacée par la valeur de la résistance au cisaillement non drainée Su. La valeur de l'angle effectif de frottement interne φ = φu est fixée à zéro, φ = 0. La surface de charge de Drucker-Prager est alors remplacée par la surface de charge de von Mises, voir ci-dessous. Cependant, les paramètres de raideur sont supposés efficaces. Dans des conditions non drainées, on s'attend généralement à ce que le sol ne subisse pas de dilatation. L'angle de dilatance ψ = 0 est donc adopté pour les deux options.
Le tableau des paramètres des matériaux montre clairement que le modèle de Drucker-Prager, tout comme le modèle élastique modifié, tient compte d'une réponse différente du sol en cas de chargement primaire et de déchargement/rechargement en introduisant le module de déchargement/rechargement Eur (voir également le modèle de Mohr-Coulomb).
Symbole | Unités | Description | |
| [MPa] | Module d'élasticité | |
| [MPa] | Module de déchargement/rechargement | |
| [-] | Coefficient de Poisson | |
| [kPa] | Coefficient effectif de cohésion | |
| [°] | Angle de frottement interne effectif | |
| [°] | Angle de dilatance | |
| [kN/m3] | Poids volumique | |
| [-] | Indice des vides initial correspondant à l'état à la fin de la première étape de calcul | |
| [-] | Taux de vide maximal pour terminer la dilatation (en cas de limitation de la dilatation) | |
| [1/K] | Coefficient de dilatation thermique (pour prendre en compte les effets de la température) |
Lors du choix des conditions non drainées Type (3): analyse en contraintes totales Su la surface de charge de Drucker-Prager est à nouveau remplacée par la surface de charge de von Mises. De même, la surface de charge de Mohr-Coulomb est remplacée par celle de Tresca. Une représentation graphique est fournie dans la figure. Cette option considère donc φ = ψ = 0, ce qui correspond à la règle d'écoulement associée. Étant donné que l'on modélise un matériau incompressible sur le plan volumétrique, la valeur du coefficient de Poisson est généralement choisie dans l'intervalle (0,49 - 0,499). Il convient de souligner qu'une valeur du coefficient de Poisson trop proche de 0,5 peut entraîner des instabilités numériques. Dans le meilleur des cas, les résultats seront très imprécis. De plus amples informations peuvent être trouvées dans le manuel théorique.
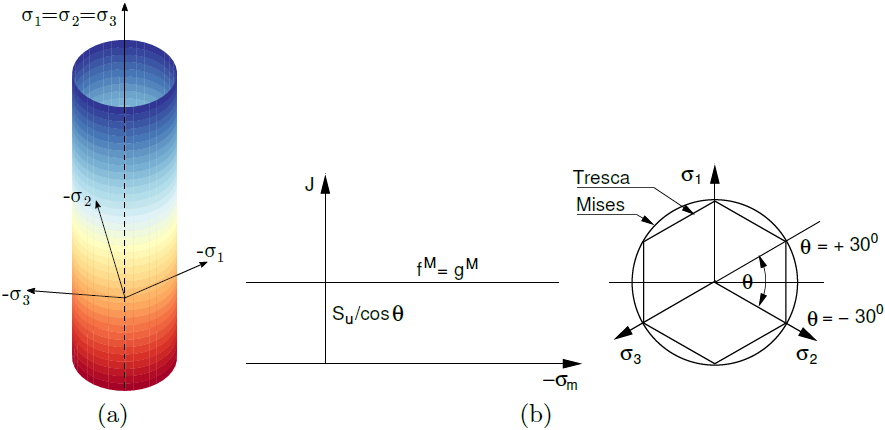 a) surface de charge dans l'espace des contraintes principales, b) projection dans le plan déviatorique c) dans le plan mériden
a) surface de charge dans l'espace des contraintes principales, b) projection dans le plan déviatorique c) dans le plan mériden
Les paramètres du matériau définissant le critère de plasticité de von Mises ou de Tresca sont donnés dans le tableau suivant. Dans le cas de le critère de plasticité de von Mises, la valeur de l'angle de Lode θ est constante à θ = ± 30°.
Symbole | Unités | Description | |
Eu | [Pa] | Module d'élasticité non drainé | |
Su | [Pa] | Résistance au cisaillement non drainé | |
ν | [-] | Coefficient de Poisson, supposé compris entre (0,49 - 0,499) | |
γ | [kN/m3] | Poids volumique | |
α | [1/K] | Coefficient de dilatation thermique (pour prendre en compte les effets de la température) |
Le modèle de Drucker-Prager permet, comme le modèle de Mohr-Coulomb, de réaliser l'analyse de stabilité. Il est possible d'effectuer à la fois l'analyse standard de la stabilité des pentes et l'analyse de la stabilité à l'intérieur d'une phase de construction donnée. Dans les deux cas, cette tâche est résolue en réduisant progressivement les paramètres de résistance au cisaillement c, φ en introduisant le paramètre de réduction ζ tel que :
![]()
où c et φ sont les paramètres réels de résistance au cisaillement et cd et φd sont les paramètres réduits. Le coefficient de sécurité FS est alors donné par :
![]()
L'angle de dilatance ψ est réduit de manière similaire dans le cas où ψ ≠ 0.
La mise en œuvre du modèle de matériau de Drucker-Prager dans le programme GEO5 MEF est décrite en détail dans le manuel théorique.