Mohr-Coulomb (MC)
Étant donné que la mécanique des sols traditionnelle et, en partie, la mécanique des roches sont basées sur ce modèle, le modèle de Mohr-Coulomb représente l'un des modèles de matériaux les plus couramment utilisés dans la pratique de l'ingénierie. Dans GEO5 MEF, la surface de limite élastique correspondante est définie à l'aide de trois fonctions limites, qui s'affichent dans l'espace des contraintes principales sous la forme d'un hexagone irrégulier. Comme pour le modèle de Drucker-Prager, la fonction d'écoulement plastique dépend de la contrainte effective moyenne σmeff. La projection de la surface de charge fMC dans le plan déviatorique montre que les arêtes individuelles se croisent en un point d'extension triaxiale θ = - 30° et de compression triaxiale θ = 30°. Comme la surface de charge dépend également de l'angle de Lode θ, le modèle est capable de fournir des prévisions qui sont en meilleur accord avec le comportement réel du sol en comparaison avec le modèle de Drucker-Prager.
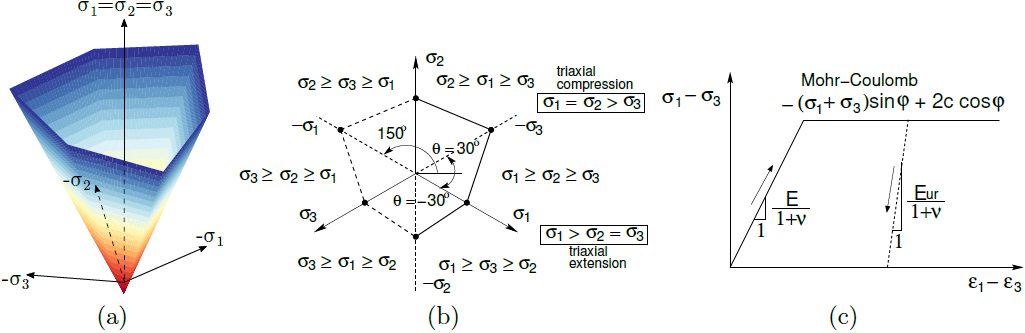 a) surface de charge dans l'espace des contraintes principales, b) projection dans le plan déviatorique c) loi contrainte-déformation
a) surface de charge dans l'espace des contraintes principales, b) projection dans le plan déviatorique c) loi contrainte-déformation
Le diagramme contrainte-déformation suggère également que le modèle de Mohr-Coulomb, tout comme le modèle élastique modifié, permet de modéliser une réponse différente du sol en cas de chargement primaire et de déchargement et rechargement ultérieurs en introduisant le module de déchargement/rechargement Eur.
Tout comme le modèle de Drucker-Prager, le modèle de Mohr-Coulomb permet de prendre en compte la dilatance du sol (évolution des déformations plastiques volumétriques positives pendant le cisaillement plastique). La solution d'une tâche donnée en conditions drainées et non drainées est également analogue. De plus amples informations, y compris la liste des paramètres matériels requis, sont disponibles dans la description du modèle de Drucker-Prager.
Un certain nombre d'exemples illustratifs, qui comparent les prévisions numériques du comportement réel du sol sur la base d'essais simples en laboratoire, sont disponibles ici. Un exemple de modélisation de conditions non drainées est fourni ici. D'autres exemples détaillés décrivant la mise en œuvre des conditions drainées et non drainées sont disponibles dans le manuel théorique.
Contrairement au modèle de Drucker-Prager, le modèle de Mohr-Coulomb, tout comme le modèle de Hoek-Brown, permet de limiter la résistance à la traction, soit en prescrivant directement la résistance à la traction σt < ccotφ, où c et φ sont des paramètres de résistance au cisaillement du sol, soit en introduisant le coefficient de réduction de la résistance à la traction TsRF. Dans ce cas, on obtient σt = TsRF × ccotφ. La réduction de la résistance à la traction est pilotée numériquement par la surface de charge de Rankine fR. La figure suivante illustre clairement ces différences.
 a) surface de charge dans l'espace des contraintes principales, b) projection dans le plan déviatorique c) projection des surfaces de charge de Mohr-Coulomb et de Rankine dans le plan σ1 - σ3
a) surface de charge dans l'espace des contraintes principales, b) projection dans le plan déviatorique c) projection des surfaces de charge de Mohr-Coulomb et de Rankine dans le plan σ1 - σ3
Le modèle de Mohr-Coulomb permet, tout comme le modèle de Drucker-Prager, de réaliser des analyses de stabilité. Il est possible d'effectuer à la fois l'analyse standard de la stabilité des pentes et l'analyse de la stabilité à l'intérieur d'une phase de construction donnée. Dans les deux cas, cette tâche est résolue en réduisant progressivement les paramètres de résistance au cisaillement c et φ en introduisant le paramètre de réduction ζ tel que :
![]()
où c et φ sont les paramètres réels de résistance au cisaillement et cd et φd sont les paramètres réduits. Le coefficient de sécurité FS est alors donné par :
![]()
L'angle de dilatance ψ est réduit de manière similaire dans le cas où ψ ≠ 0.
La mise en œuvre du modèle de matériau de Mohr-Coulomb dans le programme GEO5 MEF est décrite en détail dans le manuel théorique.